这篇介绍平常写嵌入式程序时常见的一种算法：最小二乘法。

一、最小二乘法求回归直线方程的推导过程

第一章节内容主要来自这位博主：Neo_T。

实际上我们希望这n个离差构成的总离差越小越好，只有如此才能使直线最贴近已知点。换句话说，我们求回归直线方程的过程其实就是求离差最小值的过程。

一个很自然的想法是把各个离差加起来作为总离差。可是，由于离差有正有负，直接相加会互相抵消，如此就无法反映这些数据的贴近程度，即这个总离差不能用n个离差之和来表示，见下图：

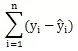
一般做法是我们用离差的平方和，即：

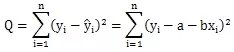
作为总离差，并使之达到最小。这样回归直线就是所有直线中Q取最小值的那一条。由于平方又叫二乘方，所以这种使“离差平方和为最小”的方法，叫做最小二乘法。
用最小二乘法求回归直线方程中的a、b的公式如下：

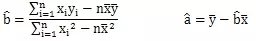
当然，我们肯定不能满足于直接得到公式，我们只有理解这个公式怎么来的才能记住它，用好它，因此给出上面两个公式的推导过程更加重要。在给出上述公式的推导过程之前，我们先给出推导过程中用到的两个关键变形公式的推导过程。首先是第一个公式：

接着是第二个公式：

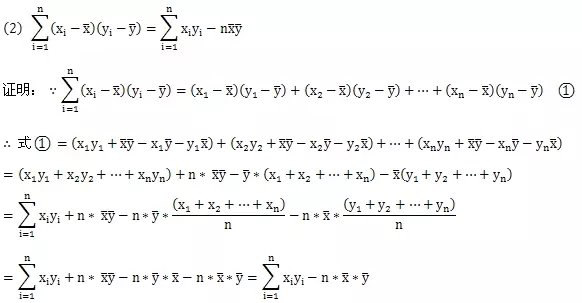
基本变形公式准备完毕，我们可以开始最小二乘法求回归直线方程公式的推导了：

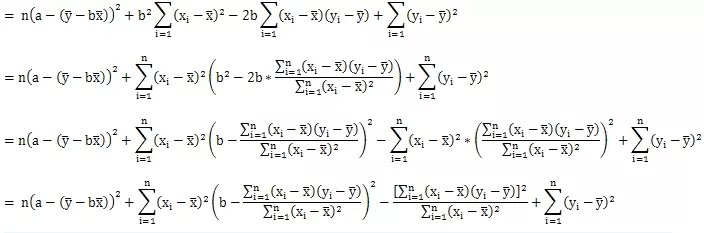
至此，公式变形部分结束，从最终式子我们可以看到后两项

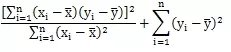
与a、b无关，属于常数项，我们只需

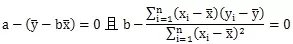
即可得到最小的Q值，因此：

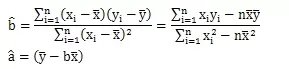
至此，公式推导完毕。

二、最小二乘法——C实现

2.1 算法代码

//-------------------------------------------------------------
//功能 : 最小二乘法直线拟合 y = a + b*x， 计算系数a 和 b
//参数 : x -- 辐照度的数组
//       y -- 功率的数组
//       num 是数组包含的元素个数，x[]和y[]的元素个数必须相等
//       a,b 都是返回值
//返回 : 拟合计算成功返回true, 拟合计算失败返回false
//-------------------------------------------------------------
voud LeastSquareLinearFit(float x[], float y[], const int num, double &a, double &b)
{
    uint64_t sum_x2 = 0;
    uint64_t sum_y  = 0;
    uint64_t sum_x  = 0;
    uint64_t sum_xy = 0;

    for(uint32_t i = 0; i < num; i++)
    {
        sum_x2 += x[i]*x[i];
        sum_y += y[i];
        sum_x += x[i];
        sum_xy += x[i]*y[i];
    }

    a = (double)(sum_x2*sum_y - sum_x*sum_xy)/(double)(num*sum_x2-sum_x*sum_x);
    b = (double)(num*sum_xy - sum_x*sum_y)/(double)(num*sum_x2 - sum_x*sum_x);

}

2.2 常见用法

最小二乘法的常见用法，就有直线拟合 & 曲线拟合。由于这里是讲解直线拟合，因此只讲直线拟合的应用场合。

直线拟合最常见、最基础的用法，实际就是求 K ，在实际的应用场合就是对应的变化率，利用 K 值大小来进行一些状态判断。例如重量的斜率K，就是重量的变化量，实际上就是流量。